안녕하세요, 박성호입니다.
오늘은 저번 SVM으로 분류를 해보았는데요, 이번엔 회귀 SVM인 SVR (Support Vector Regression)을 공부해보겠습니다!
□ SVR이란
앞서 이야기한 것처럼 SVM 알고리즘은 다목적으로 사용할 수 있습니다.
선형, 비선형 회귀에서도 사용할 수 있습니다. SVM 분류가 아니라 회귀에서 적용하는 방법은 목표를 반대로 하는 것입니다.
일정한 마진 오류안에서 두 클래스 간의 도로 폭이 가능한 한 최대가 되도록 하는 대신,
SVM회귀는 제한된 마진 오류 (즉, 도로밖의 샘플) 안에서 도로 안에 가능한 한 많은 샘플이 들어가도록 학습합니다.
사이킷런의 LinearSVR을 사용해 선형 SVR 회귀를 적용해보겠습니다.
import numpy as np
np.random.seed(42)
m = 50
X = 2 * np.random.rand(m, 1)
y = (4 + 3 * X + np.random.randn(m, 1)).ravel()
from sklearn.svm import LinearSVR
svm_reg = LinearSVR(epsilon=1.5, random_state=42)
svm_reg.fit(X, y)
svm_reg1 = LinearSVR(epsilon=1.5, random_state=42)
svm_reg2 = LinearSVR(epsilon=0.5, random_state=42)
svm_reg1.fit(X, y)
svm_reg2.fit(X, y)
def find_support_vectors(svm_reg, X, y):
y_pred = svm_reg.predict(X)
off_margin = (np.abs(y - y_pred) >= svm_reg.epsilon)
return np.argwhere(off_margin)
svm_reg1.support_ = find_support_vectors(svm_reg1, X, y)
svm_reg2.support_ = find_support_vectors(svm_reg2, X, y)
eps_x1 = 1
eps_y_pred = svm_reg1.predict([[eps_x1]])
def plot_svm_regression(svm_reg, X, y, axes):
x1s = np.linspace(axes[0], axes[1], 100).reshape(100, 1)
y_pred = svm_reg.predict(x1s)
plt.plot(x1s, y_pred, "w-", linewidth=2, label=r"$\hat{y}$")
plt.plot(x1s, y_pred + svm_reg.epsilon, "w--")
plt.plot(x1s, y_pred - svm_reg.epsilon, "w--")
plt.scatter(X[svm_reg.support_], y[svm_reg.support_], s=180, facecolors='#FFAAAA')
plt.plot(X, y, "bo", marker='X', c='c')
plt.xlabel(r"$x_1$", fontsize=18)
plt.legend(loc="upper left", fontsize=18)
plt.axis(axes)
fig, axes = plt.subplots(ncols=2, figsize=(9, 4), sharey=True)
plt.sca(axes[0])
plot_svm_regression(svm_reg1, X, y, [0, 2, 3, 11])
plt.title(r"$\epsilon = {}$".format(svm_reg1.epsilon), fontsize=18)
plt.ylabel(r"$y$", fontsize=18, rotation=0)
#plt.plot([eps_x1, eps_x1], [eps_y_pred, eps_y_pred - svm_reg1.epsilon], "k-", linewidth=2)
plt.annotate(
'', xy=(eps_x1, eps_y_pred), xycoords='data',
xytext=(eps_x1, eps_y_pred - svm_reg1.epsilon),
textcoords='data', arrowprops={'arrowstyle': '<->', 'linewidth': 1.5}
)
plt.text(0.91, 5.6, r"$\epsilon$", fontsize=20)
plt.sca(axes[1])
plot_svm_regression(svm_reg2, X, y, [0, 2, 3, 11])
plt.title(r"$\epsilon = {}$".format(svm_reg2.epsilon), fontsize=18)
save_fig("svm_regression_plot")
plt.show()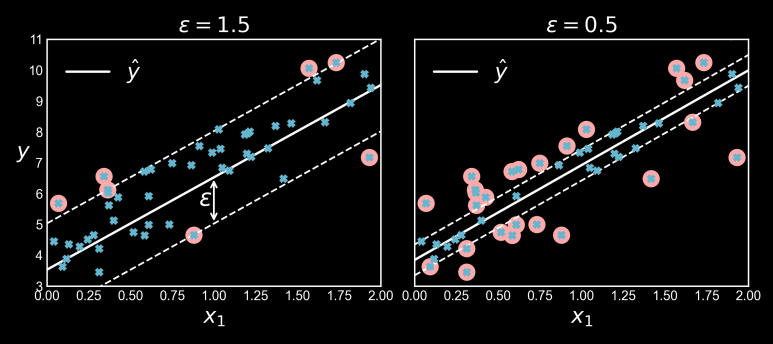
도로의 폭은 하이퍼파라미터 epsilon으로 조절합니다.
위의 그림에서 무작위로 생성한 선형 데이터셋에 훈련시킨 두 개의 선형 SVM 회귀 모델을 보여줍니다
하나는 마진을 크게 (epsilon=1.5)하고 다른 하나는 마진을 작게 (epsilon=0.5)하여 만들었습니다.
보이는 것과 같이 마진안에서는 훈련 샘플이 추가되어도 모델의 예측에는 영향이 없습니다.
그래서 이 모델을 epsilon에 민감하지 않다(epsilon-insensitive)고 말합니다.
np.random.seed(42)
m = 100
X = 2 * np.random.rand(m, 1) - 1
y = (0.2 + 0.1 * X + 0.5 * X**2 + np.random.randn(m, 1)/10).ravel()
from sklearn.svm import SVR
svm_poly_reg1 = SVR(kernel="poly", degree=2, C=100, epsilon=0.1, gamma="scale")
svm_poly_reg2 = SVR(kernel="poly", degree=2, C=0.01, epsilon=0.1, gamma="scale")
svm_poly_reg1.fit(X, y)
svm_poly_reg2.fit(X, y)
fig, axes = plt.subplots(ncols=2, figsize=(9, 4), sharey=True)
plt.sca(axes[0])
plot_svm_regression(svm_poly_reg1, X, y, [-1, 1, 0, 1])
plt.title(r"$degree={}, C={}, \epsilon = {}$".format(svm_poly_reg1.degree, svm_poly_reg1.C, svm_poly_reg1.epsilon), fontsize=18)
plt.ylabel(r"$y$", fontsize=18, rotation=0)
plt.sca(axes[1])
plot_svm_regression(svm_poly_reg2, X, y, [-1, 1, 0, 1])
plt.title(r"$degree={}, C={}, \epsilon = {}$".format(svm_poly_reg2.degree, svm_poly_reg2.C, svm_poly_reg2.epsilon), fontsize=18)
save_fig("svm_with_polynomial_kernel_plot")
plt.show()
비선형 회귀 작업을 처리하려면 커널 SVM 모델을 사용합니다.
위의 그림은 2차방정식 형태의 훈련세트에 2차 다항 커널을 사용한 SVM 회귀를 보여줍니다.
왼쪽 그래프는 규제가 거의 없고 (즉, 아주 큰 C), 오른쪽 그래프는 규제가 훨씬 많습니다(즉, 작은 C)
svm_rbf_reg1 = SVR(kernel="rbf", C=100, epsilon=0.1, gamma="scale")
svm_rbf_reg2 = SVR(kernel="rbf", C=0.01, epsilon=0.1, gamma="scale")
svm_rbf_reg1.fit(X, y)
svm_rbf_reg2.fit(X, y)
fig, axes = plt.subplots(ncols=2, figsize=(9, 4), sharey=True)
plt.sca(axes[0])
plot_svm_regression(svm_rbf_reg1, X, y, [-1, 1, 0, 1])
plt.title(r"$degree={}, C={}, \epsilon = {}$".format(svm_rbf_reg1.degree, svm_rbf_reg1.C, svm_rbf_reg1.epsilon), fontsize=18)
plt.ylabel(r"$y$", fontsize=18, rotation=0)
plt.sca(axes[1])
plot_svm_regression(svm_rbf_reg2, X, y, [-1, 1, 0, 1])
plt.title(r"$degree={}, C={}, \epsilon = {}$".format(svm_rbf_reg2.degree, svm_rbf_reg2.C, svm_rbf_reg2.epsilon), fontsize=18)
plt.show()
이렇게 rbf 커널도 가능하여 해당 데이터셋에서 성능이 좋은 커널을 쓰시는게 좋아보입니다.
□ SVR 실습 - Boston 데이터
from sklearn import datasets
import pandas as pd
boston = datasets.load_boston()
df_boston = pd.DataFrame(boston.data,columns=boston.feature_names)
df_boston['target'] = pd.Series(boston.target)
df_boston.head(5)
correlation_matrix = df_boston.corr().round(2)
plt.subplots(figsize=(20,15))
sns.heatmap(data=correlation_matrix, annot=True, cmap="bwr")
plt.show()
plt.subplots(1,4, figsize=(20, 5))
features = ['LSTAT', 'RM', 'PTRATIO', 'INDUS']
target = boston.target
for i, col in enumerate(features):
plt.subplot(1, len(features), i + 1)
x = df_boston[col]
y = target
plt.scatter(x, y, marker='o')
plt.title(col)
plt.xlabel(col)
plt.ylabel('MEDV')
plt.show()
# 독립변수에 LSTAT만 남기고 모두 drop 합니다
X = df_boston.drop(['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX','PTRATIO' , 'B' , 'target'], axis=1)
Y = df_boston.iloc[:, -1].values
X,Y
>>> ( LSTAT
0 4.98
1 9.14
2 4.03
3 2.94
4 5.33
.. ...
501 9.67
502 9.08
503 5.64
504 6.48
505 7.88
[506 rows x 1 columns],
array([24. , 21.6, 34.7, 33.4, 36.2, 28.7, 22.9, 27.1, 16.5, 18.9, 15. ,
18.9, 21.7, 20.4, 18.2, 19.9, 23.1, 17.5, 20.2, 18.2, 13.6, 19.6,
.....................
20.6, 21.2, 19.1, 20.6, 15.2, 7. , 8.1, 13.6, 20.1, 21.8, 24.5,
23.1, 19.7, 18.3, 21.2, 17.5, 16.8, 22.4, 20.6, 23.9, 22. , 11.9]))# 학습 검증 분할
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.2, random_state=5)
# svr 모델
from sklearn.svm import SVR
from sklearn.svm import LinearSVR
svr_rbf_reg = SVR(kernel="rbf", C=100)
svr_rbf_reg.fit(X_train, y_train)
print("test data 예측값:\n", svr_rbf_reg.predict(X_test))
>>> test data 예측값:
[40.99387782 31.65143929 22.08127141 8.92934489 24.68292155 13.30421812
27.51026542 22.50073441 21.78363984 19.25466526 25.70011328 21.85626122
21.81688531 23.94463763 22.79156555 20.73749388 8.54864551 20.25939039
.....................
32.96417054 19.76799132 20.40044317 16.96127854 23.26914015 28.94161221
16.2534109 26.63150726 17.53233503 17.41907141 21.66055173 21.89603755]plt.figure(figsize=(20,8))
# -3과 3 사이에 1000개의 데이터 포인트를 만듭니다.
line = np.linspace(0, 40, 1000).reshape(-1,1)
#모델링 결과
plt.plot(X_train, y_train, 'd', c='b', markersize=8)
plt.plot(X_test, y_test, 'o', c='r', alpha=0.6, markersize=10)
plt.plot(line, svr_rbf_reg.predict(line), c='mintcream')
plt.legend(["훈련 데이터/타깃", "검증 데이터/타깃", "모델 예측"], loc="best")
# R-square 모델 성능 평가
print("테스트 셋 R-square : {:.4f}".format(svr_rbf_reg.score(X_test, y_test)))
>>> 테스트 셋 R-square : 0.6149from sklearn.neighbors import KNeighborsRegressor
knn_reg5 = KNeighborsRegressor(n_neighbors=5)
knn_reg5.fit(X_train, y_train)
print("test data 예측값:\n", knn_reg5.predict(X_test))
print("테스트 셋 R-square : {:.4f}".format(knn_reg5.score(X_test, y_test)))
>>> test data 예측값:
[45.16 32.9 27.36 10.24 26.2 12.1 26.32 26.16 20.7 17.82 26.16 23.76
23.2 26.48 26.32 19.3 10.24 21.14 13.66 20.92 14.58 22.18 34.12 20.74
22.78 13. 25.62 19.6 25.98 25.34 12.92 13.4 16.8 15.7 22.52 20.04
28.6 13.24 26.06 45.62 17.36 10.24 28.04 19.5 28.72 25.72 10.24 16.68
19.78 13.24 20.18 21.48 28.7 11.88 17.88 26.3 33.38 16.62 25.6 19.66
19.64 20.92 14.06 36.26 20.38 14.1 21.48 28.72 23.6 20.38 17.88 26.
16.7 14.1 19.22 31.16 17.26 14.78 21.22 17.88 21.32 40.88 14.78 17.36
19.86 17.24 17.36 12.2 17.88 23.2 29.9 21.56 20.38 15.6 32.76 29.44
15.28 26.06 17.54 16.7 21.4 28.6 ]
테스트 셋 R-square : 0.5967plt.figure(figsize=(15,8))
plt.plot(X_train, y_train, 'd', c='b', markersize=8)
plt.plot(X_test, y_test, 'o', c='r', markersize=10)
plt.plot(line, knn_reg5.predict(line), c='mintcream')
plt.legend(["훈련 데이터/타깃", "검증 데이터/타깃", "모델 예측"], loc="best")
하나의 독립변수를 썻고 파라미터의 조정이 필요하겠지만 KNN의 R-square값은 0.5967, SVR의 R-square값은 0.6149로 SVR의 성능이 비교적 우수한 것으로 출력되었네요. 이로써 KNN의 단점, 이웃에 의해 학습하기 때문에 이상치에 민감하다는 단점을 SVR에서 커버할 수 있을 것 같다는 제 주관을 끝으로, 이상으로 [Python/ML] SVR (Support Vector Regression)를 마치도록 하겠습니다..
오늘도 긴 글 읽어주셔서 대단히 감사드립니다.
'Data Park > Python' 카테고리의 다른 글
| [Python/ML] DBSCAN Clustering (2) | 2023.02.03 |
|---|---|
| [Python/ML] Agglomerative Hierarchical Clustering (계층적 군집화) (2) | 2023.01.28 |
| [Python/ML] K-MEANS Clustering (0) | 2023.01.27 |
| [Python/ML] K-NN (K-Nearest Neighbors) (0) | 2023.01.10 |
| [Python/ML] SVM (Support Vector Machine) (0) | 2023.01.04 |



