안녕하세요, 원주 기술코치 박성호입니다.
오늘은 K-MEANS에 이어 계층적 군집화, Agglomerative Hierarchical Clustering에 대해서 글을 쓰게 되었네요.
바로 들어가보도록 하죠!
□ Agglomerative Hierarchical Clustering(계층적 군집화) 개념
계층적 군집화는 말 그대로 데이터 하나하나를 계층에 따라 순차적으로 클러스터링 하는 기법입니다.
이 알고리즘은 각 데이터가 모두 나눠져있는 상태에서, 작은 단위로부터 클러스터링을 시작하여 모든 데이터를 묶을 때까지 반복하여 군집화를 진행합니다.
다음과 같이 12개의 index가 부여된 데이터가 있다고 가정하고,
# 군집할 데이터 생성
from sklearn.dataset import make_blobs
X, y = make_blobs(random_state=0, n_samples=12)
n=12
# 산점도, index 라벨링
import matplotlib.pyplot as plt
plt.plot(X[:,0],X[:,1],'ro')
for i in range(X.shape[0]):
plt.text(X[i,0], X[i,1], str(i),)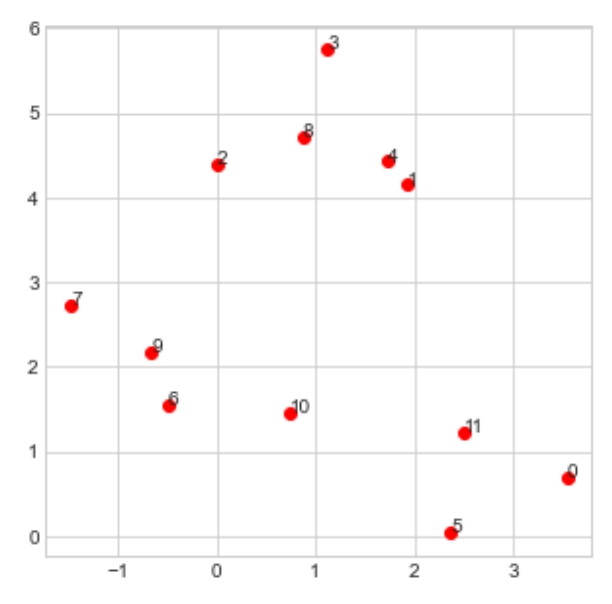
계층적 군집화는 어떠한 매커니즘으로 군집이 되는지 알아봅시다.
mglearn.plots.plot_agglomerative_algorithm()
for i in range(X.shape[0]):
plt.text(X[i,0], X[i,1], str(i))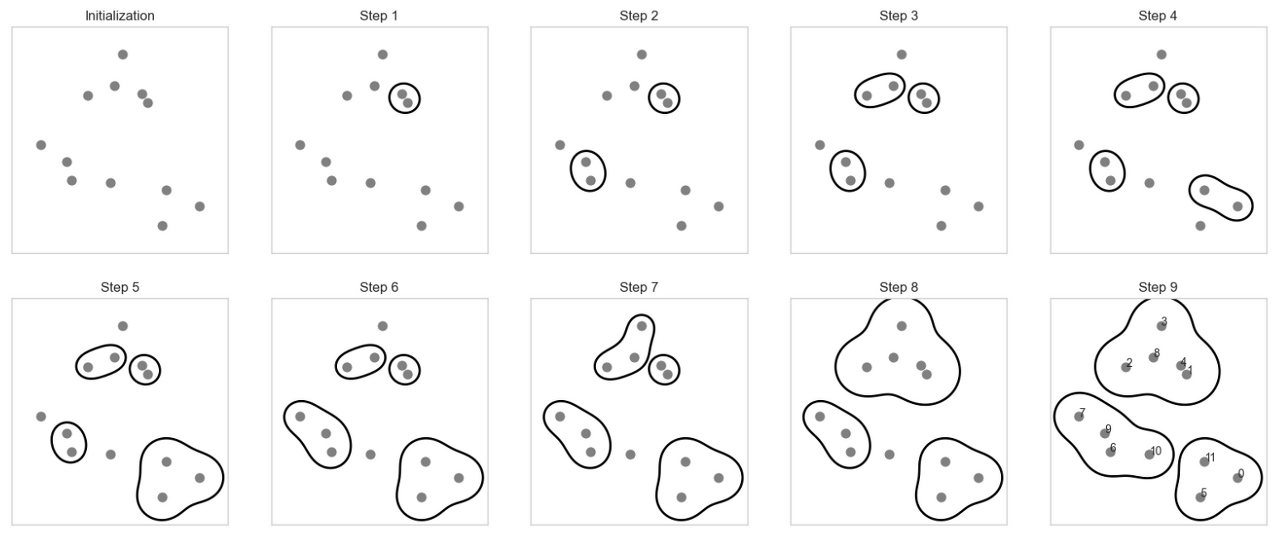
[step 1], 제일 가까운 데이터를 찾고 그들을 묶는다.
제일 가까운 데이터는 1,4 데이터이고 그 둘을 하나의 군집으로 묶는다.
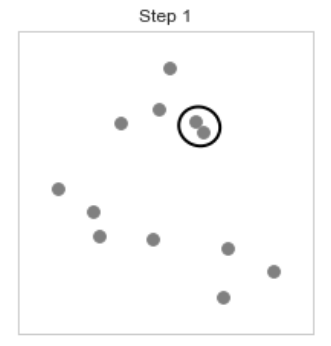
[step 2], 다음으로 같은 방식으로 가장 가까운 거리의 9,6 데이터를 묶는다
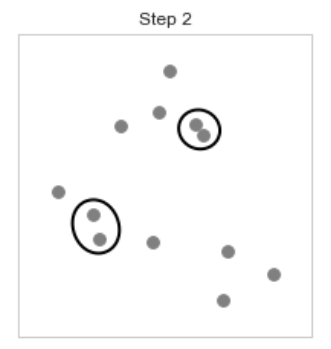
[step 3,4] 방금 [step 1,2]에서 했던 방식으로 반복하여 2,8 데이터, 11,0 데이터도 묶는다
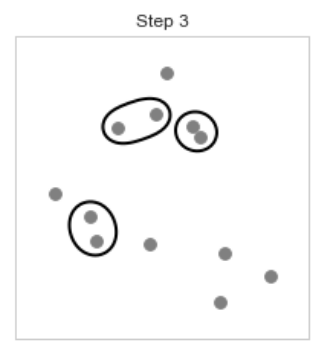
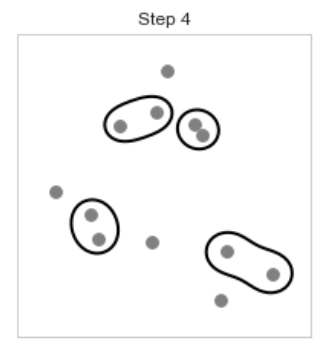
[step 5] 다음으로 묶을 데이터는 5번 데이터인데 [step 4]에서 묶인 11,0 클러스터와 가장 가까워 11,0 데이터와 묶어준다.
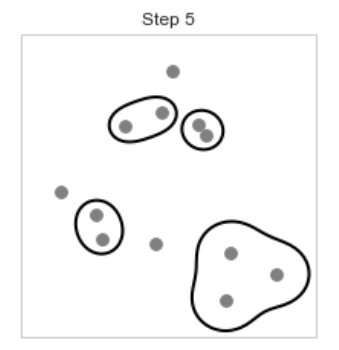
[step 6, 7] 다음 [step 5]에서 묶은 방식과 동일하게 7번 데이터는 9,6클러스터와, 3번 데이터는 8,2 클러스터와 묶어준다.
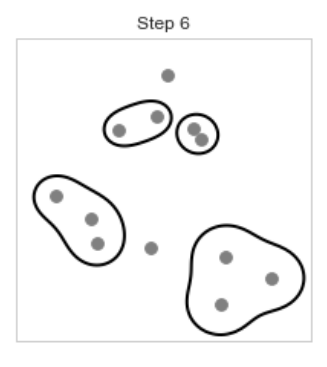
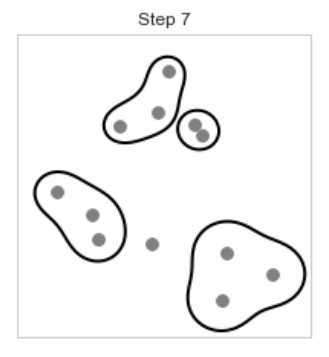
[Step 8] 다음으로 2,8,3 클러스터와 4,1클러스터가 가까워 이 두 클러스터는 하나의 클러스터로 묶인다.
(클러스터와 데이터, 클러스터와 클러스터 사이의 거리 측정 방법(linkage parameter)은 아래에서 설명합니다.)
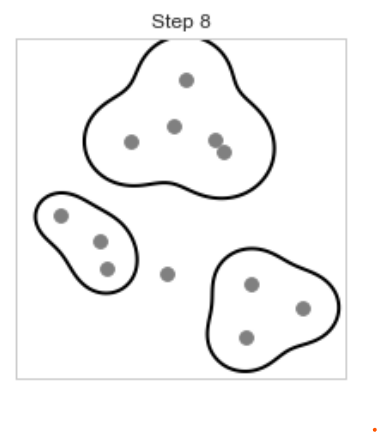
[Step 9] 이런 식으로 모든 데이터가 하나의 클러스터로 묶일 때까지 알고리즘을 반복하면 아래와 같은 결과가 생성된다.
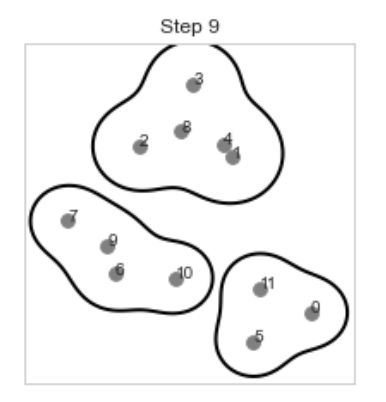
from sklearn import cluster
from sklearn.cluster import AgglomerativeClustering
X,y = make_blobs(random_state=0, n_samples=12)
agg = AgglomerativeClustering(n_clusters=3)
assignmeant = agg.fit_predict(X)
mglearn.discrete_scatter(X[:,0],X[:,1], assignmeant, s=17)
mglearn.plots.plot_agglomerative()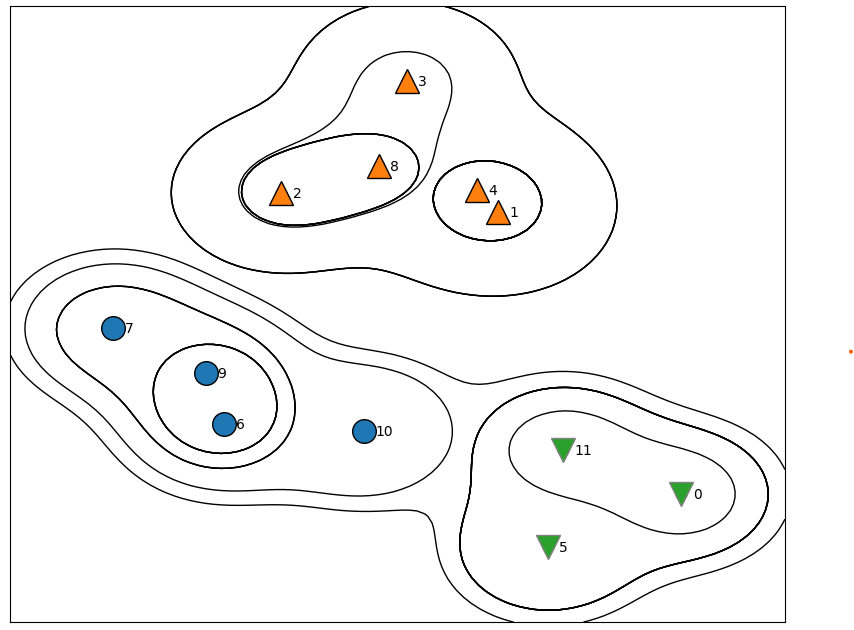
이 그래프는 계층군집의 모습을 자세히 나타내지만 2차원 데이터일때 뿐이며 특성이 셋이상인 데이터셋에서는 사용할 수 없습니다.
하지만 계층군집을 시각화하는 또 다른 도구인 덴드로그램은 다차원 데이터셋을 처리할 수 있습니다.
아쉽게도 scikit-learn은 아직까지 덴드로그램을 그리는 기능을 제공하지 않지만, SciPy를 사용해 손쉽게 만들 수 있습니다.
SciPy에서 ward 군집 함수와 덴드로그램 함수를 임포트합니다.
from scipy.cluster.hierarchy import dendrogram, ward
# 데이터 배열 X에 ward함수를 적용합니다.
# SciPy의 ward함수는 병합 군집을 수행할 때 생성된 거리정보가 담긴 배열을 반환합니다
linkage_array = ward(X)
# 클러스터 간의 거리 정보가 담긴 linkage_array를 사용해 덴드로그램을 그립니다.
dendrogram(linkage_array)
# 2개와 3개의 클러스터를 구분하는 커트라인 표시
ax = plt.gca()
bounds = ax.get_xbound()
ax.plot(bounds, [7.25, 7.25], '--', c='k')
ax.plot(bounds, [4, 4], '--', c='k')
ax.text(bounds[1], 7.25, '2 cluster', va='center', bbox=dict(facecolor='red', alpha=0.5), fontdict={'size':15})
ax.text(bounds[1], 4, '3 cluster', va='center', bbox=dict(facecolor='red', alpha=0.5), fontdict={'size':15})
plt.xlabel("sample ID")
plt.ylabel("cluster distance")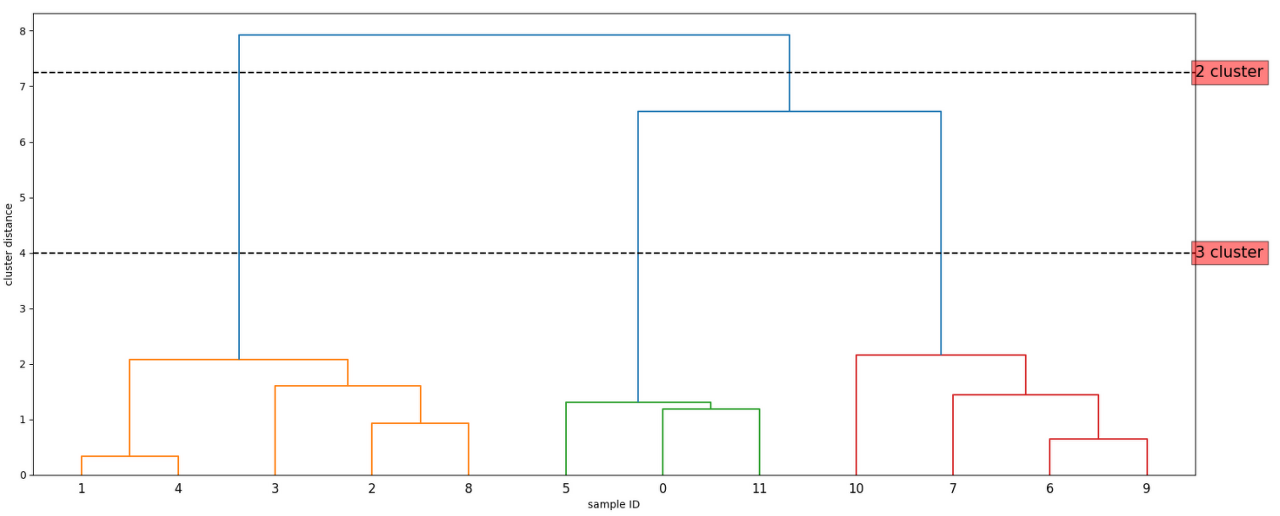
이때 덴드로그램의 수평선 높이는 만들어진 순서대로 정해집니다. 우리의 예시에서는 1,4클러스터가 가장 먼저 하나의 클러스터로 묶이고 다음으로 9,6클러스터, 0,11클러스터가 묶였기때문에 2,8클러스터의 가로선이 가장 아래, 9,6클러스터가 그 위, 0,11클러스터가 그 위의 순서가 됩니다.
□ Cluster의 거리 측정
이러한 계층적 군집화에서 클러스터와 클러스터 사이의 거리는 어떻게 측정할 것인가?
거리 측정방식은 AgglomerativeClustering에서 "linkage"라는 파라미터로 설명이 가능합니다.

이 측정은 항상 클러스터 사이에서 이뤄집니다.
ward
: 병합되는 군집의 분산을 최소화합니다.
single
: 군집의 데이터간 거리의 평균을 사용합니다.
complete
: 군집내의 모든 데이터 사이의 최대 거리를 사용합니다.
single
: 군집내의 모든 관측치 사이의 최소 거리를 사용합니다.
□ Agglomerative Clustering 실습
알고리즘의 작동 특성상 병합 군집은 새로운 데이터 포인트에 대해서는 예측을 할수 없습니다.
그러므로 병합 군집은 predict 메서드가 없습니다. 대신 훈련 셋트로 모델을 만들고 클러스터 소속 정보를 얻기 위해 fit_predict 메서드를 사용합니다.
저번에 업로드했던 K-Means와 알고리즘 비교를 위해 같은 데이터를 쓰겠습니다.
# 데이터 생성
X, y = make_blobs(random_state=1)
X, y
>>> (array([[-7.94152277e-01, 2.10495117e+00],
[-9.15155186e+00, -4.81286449e+00],
[-1.14418263e+01, -4.45781441e+00],
[-9.76761777e+00, -3.19133737e+00],
# 생략
[-6.50212109e+00, -7.91249101e+00],
[-1.02639310e+01, -3.92073400e+00],
[-6.81608302e+00, -8.44986926e+00],
[-1.34052081e+00, 4.15711949e+00],
[-1.03729975e+01, -4.59207895e+00],
[ 8.52518583e-02, 3.64528297e+00]]),
array([0, 1, 1, 1, 2, 2, 2, 1, 0, 0, 1, 1, 2, 0, 2, 2, 2, 0, 1, 1, 2, 1,
# 생략
2, 0, 1, 2, 2, 0, 0, 2, 0, 0, 2, 0, 1, 2, 1, 1, 1, 2, 2, 1, 0, 1,
1, 0, 2, 0, 0, 1, 1, 2, 2, 0, 2, 0]))군집화는 비지도 학습이기 때문에 레이블 y값은 무시하고 산점도를 그려보았고
# 산점도
mglearn.discrete_scatter(X[:,0],X[:,1])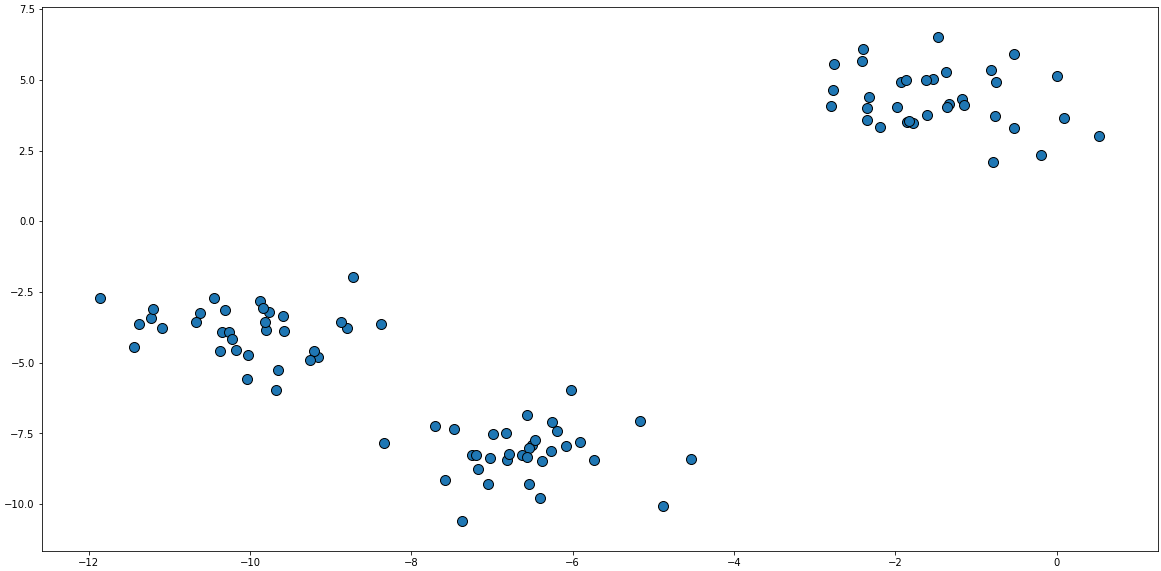
이 데이터를 AgglomerativeClustering으로 군집화시킵니다.
# 모델 생성
agg = AgglomerativeClustering(n_clusters=3)
# 군집화 수행
assignmeant = agg.fit_predict(X)
# 군집 결과 출력
assignmeant
>>> array([0, 2, 2, 2, 1, 1, 1, 2, 0, 0, 2, 2, 1, 0, 1, 1, 1, 0, 2, 2, 1, 2,
1, 0, 2, 1, 1, 0, 0, 1, 0, 0, 1, 0, 2, 1, 2, 2, 2, 1, 1, 2, 0, 2,
2, 1, 0, 0, 0, 0, 2, 1, 1, 1, 0, 1, 2, 2, 0, 0, 2, 1, 1, 2, 2, 1,
0, 1, 0, 2, 2, 2, 1, 0, 0, 2, 1, 1, 0, 2, 0, 2, 2, 1, 0, 0, 0, 0,
2, 0, 1, 0, 0, 2, 2, 1, 1, 0, 1, 0], dtype=int64)이전에 말씀드린 것처럼 K-MEANS와 달리 AgglomerativeClustering 알고리즘 작동특성상 fit_predict 메서드를 사용하여 군집 결과를 출력해냅니다.
# 군집 결과 산점도
mglearn.discrete_scatter(X[:,0],X[:,1], assignmeant)
# 범례, 제목 추가
plt.legend(["Cluster 0", "Cluster 1", "Cluster 2"], loc="best")
plt.title("AgglomerativeClustering")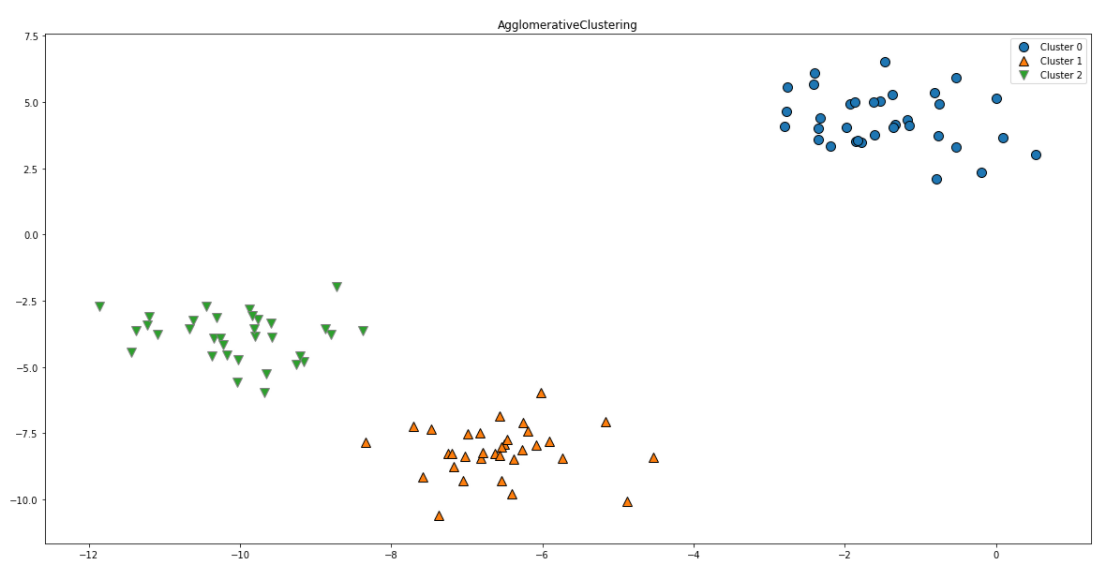
from scipy.cluster.hierarchy import dendrogram, ward
linkage_array = ward(X)
dendrogram(linkage_array)
ax = plt.gca()
bounds = ax.get_xbound()
ax.plot(bounds, [65, 65], '--', c='k')
ax.plot(bounds, [25, 25], '--', c='k')
ax.text(bounds[1], 65, '2 cluster', va='center', bbox=dict(facecolor='red', alpha=0.5), fontdict={'size':15})
ax.text(bounds[1], 25, '3 cluster', va='center', bbox=dict(facecolor='red', alpha=0.5), fontdict={'size':15})
plt.xlabel("sample ID")
plt.ylabel("cluster distance")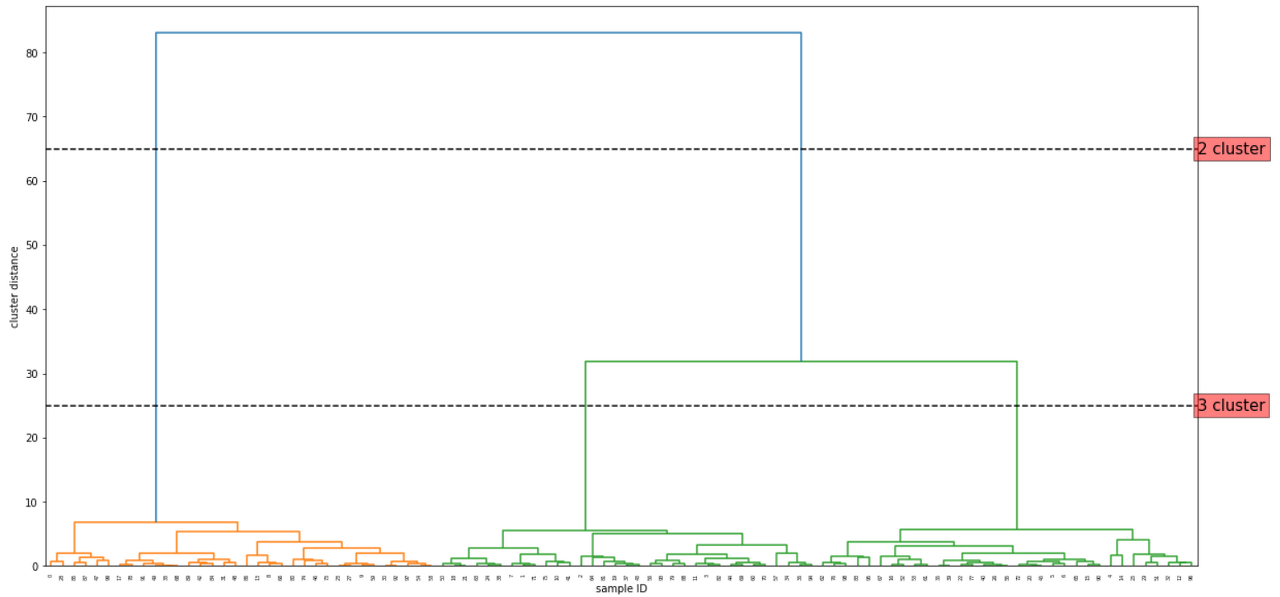
이렇게 K-MEANS와 큰 차이는 보이지 않는 것 같지만 AgglomerativeClustering은 군집 중심점이 없고 클러스터와 데이터간의 거리로 군집을 하기때문에 다소 복잡한 형태도 잘 군집을 해냅니다,
K-means와 달리 복잡한 데이터셋도 군집해내는 것을 보여드리기위해 다양한 데이터셋을 군집시켜보겠습니다!
# 데이터 생성 라이브러리 불러오기
from sklearn.datasets import make_blobs
from sklearn.datasets import make_moons
from sklearn.datasets import make_circles
import numpy as np
# 데이터 생성
X_c, y_c = make_circles(n_samples=300, factor=0.3, noise=0.1, random_state=0)
X_m,y_m = make_moons(n_samples=300, noise=0.05, random_state=0)
X_r,y_r = make_blobs(random_state=9, n_features=3, n_samples=600, cluster_std=[1.0, 2.0, 0.5])
X,y = make_blobs(random_state=170, n_samples=600)
rng = np.random.RandomState(74)
transformation = rng.normal(size=(2,2))
X_trm = np.dot(X, transformation)이렇게 생성한 5개의 데이터셋을 산점도로 그려봅니다.
fig, axes = plt.subplots(1,5, figsize=(40,10))
mglearn.discrete_scatter(X_c[:,0],X_c[:,1],s=20, markeredgewidth=2, ax=axes[0])
mglearn.discrete_scatter(X_m[:,0],X_m[:,1], s=20 ,markeredgewidth=2, ax=axes[1])
mglearn.discrete_scatter(X_trm[:,0],X_trm[:,1], s=20 ,markeredgewidth=2, ax=axes[2])
mglearn.discrete_scatter(X_r[:,0],X_r[:,1], s=20 ,markeredgewidth=2, ax=axes[3])
mglearn.discrete_scatter(X[:,0],X[:,1], s=20 ,markeredgewidth=2, ax=axes[4])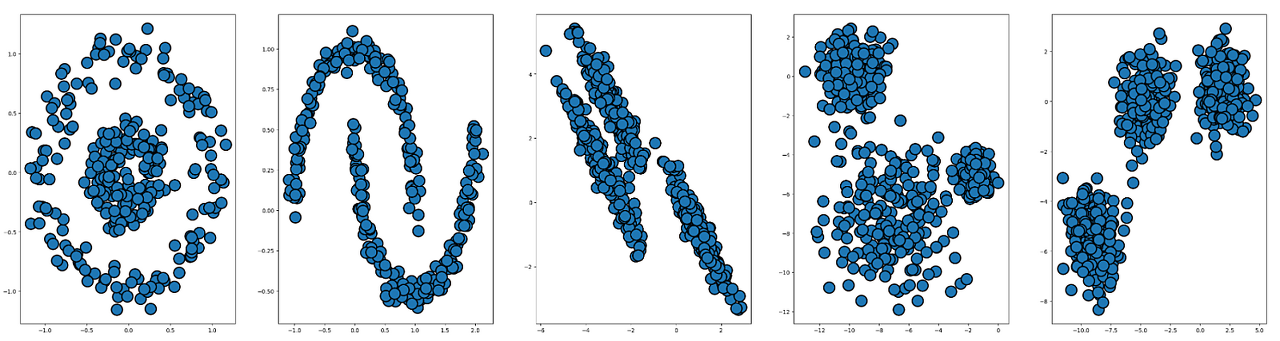
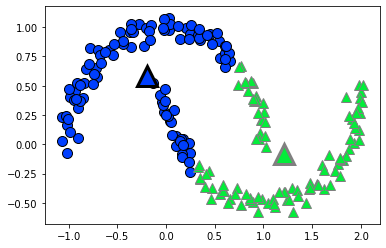
저번 K-means 군집화는 이렇게 원형의 반경으로 군집을 하는데 계층적 군집화는 moons data를 어떻게 군집할까요
fig, axes = plt.subplots(1,4, figsize=(40,10))
# linkage = 'ward' (디폴트값)
agg = AgglomerativeClustering(n_clusters=2)
assignmeant = agg.fit_predict(X_m)
mglearn.discrete_scatter(X_m[:,0],X_m[:,1], assignmeant, s=20 ,ax=axes[0])
# linkage = 'complete'
agg1 = AgglomerativeClustering(n_clusters=2, linkage='complete')
assignmeant1 = agg1.fit_predict(X_m)
mglearn.discrete_scatter(X_m[:,0],X_m[:,1], assignmeant1, s=20 ,ax=axes[1])
# linkage='average'
agg2 = AgglomerativeClustering(n_clusters=2, linkage='average')
assignmeant2 = agg2.fit_predict(X_m)
mglearn.discrete_scatter(X_m[:,0],X_m[:,1], assignmeant2, s=20 ,ax=axes[2])
# linkage='single'
agg3 = AgglomerativeClustering(n_clusters=2, linkage='single')
assignmeant3 = agg3.fit_predict(X_m)
mglearn.discrete_scatter(X_m[:,0],X_m[:,1], assignmeant3, s=20 ,ax=axes[3])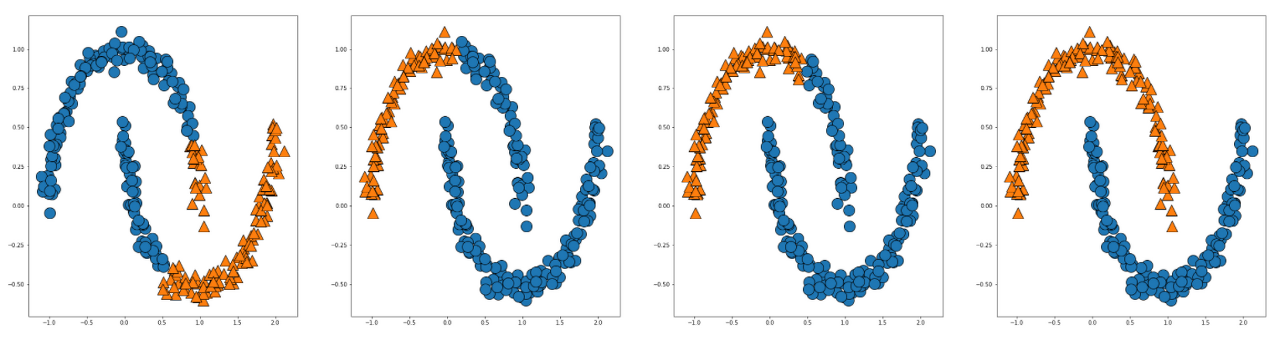
4번째 plot에 linkage = 'single' 로 군집한 결과가 잘 군집한 것으로 보입니다.
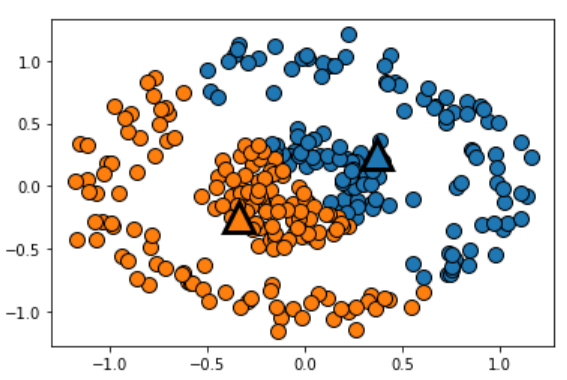
위의 사진은 k-means의 circles data 군집 결과이고, 반면, 계층적 군집화는 circles data에서 잘 작동할까요
fig, axes = plt.subplots(1,4, figsize=(40,10))
# linkage = 'ward' (디폴트값)
agg = AgglomerativeClustering(n_clusters=2)
assignmeant = agg.fit_predict(X_c)
mglearn.discrete_scatter(X_c[:,0],X_c[:,1], assignmeant, s=20 ,ax=axes[0])
# linkage = 'complete'
agg1 = AgglomerativeClustering(n_clusters=2, linkage='complete')
assignmeant1 = agg1.fit_predict(X_c)
mglearn.discrete_scatter(X_c[:,0],X_c[:,1], assignmeant1, s=20 ,ax=axes[1])
# linkage='average'
agg2 = AgglomerativeClustering(n_clusters=2, linkage='average')
assignmeant2 = agg2.fit_predict(X_c)
mglearn.discrete_scatter(X_c[:,0],X_c[:,1], assignmeant2, s=20 ,ax=axes[2])
# linkage='single'
agg3 = AgglomerativeClustering(n_clusters=2, linkage='single')
assignmeant3 = agg3.fit_predict(X_c)
mglearn.discrete_scatter(X_c[:,0],X_c[:,1], assignmeant3, s=20 ,ax=axes[3])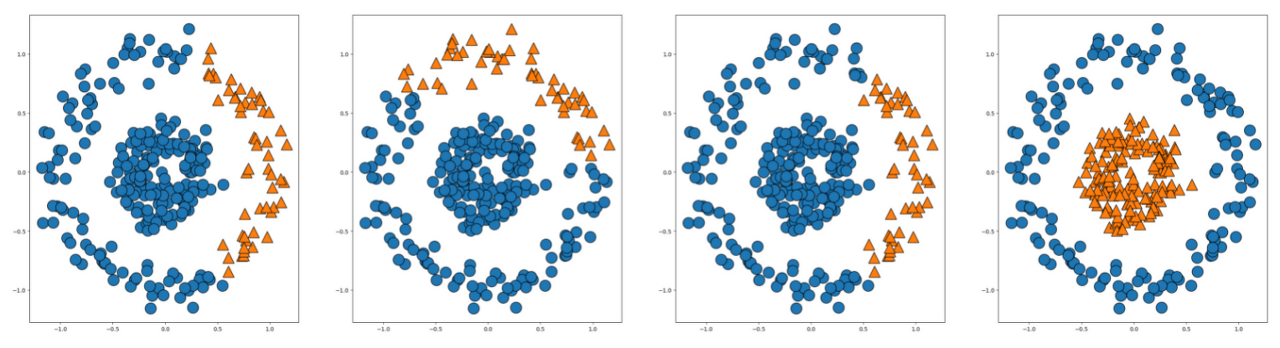
two circles 데이터셋도 linkage = 'single' 로 군집한 결과가 잘 군집한 것으로 보입니다.
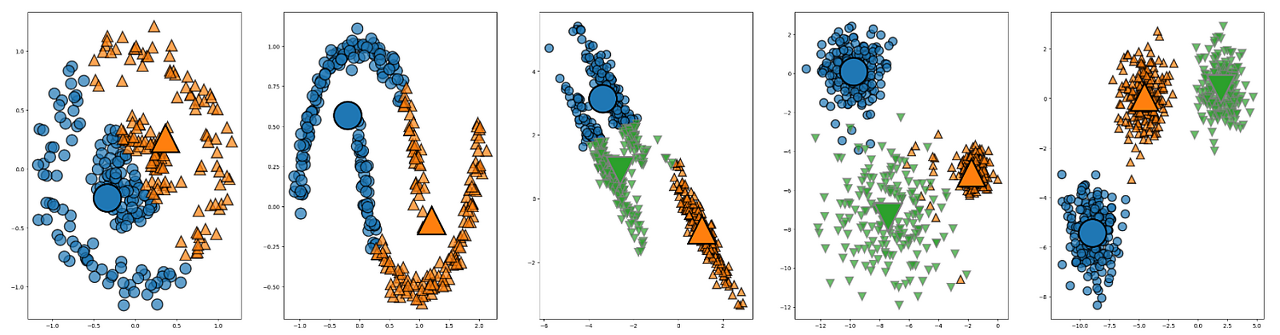
위의 데이터는 K-MEANS로 다섯종류의 데이터를 군집한 결과입니다.
K-MEANS는 two_circles과 two_moons dataset을 transformed dataset은 군집이 어려워보입니다
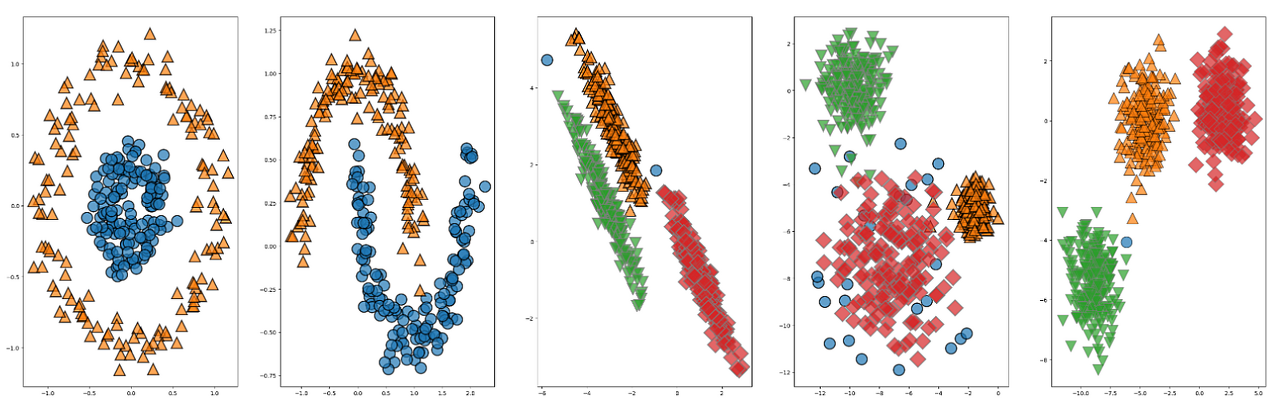
fig, axes = plt.subplots(1,5, figsize=(40,10))
agg_c = AgglomerativeClustering(n_clusters=2, linkage='single')
assignmeant_c = agg_c.fit_predict(X_c)
mglearn.discrete_scatter(X_c[:,0],X_c[:,1], assignmeant_c, s=20 ,ax=axes[0])
agg_m = AgglomerativeClustering(n_clusters=2, linkage='single')
assignmeant_m = agg_m.fit_predict(X_m)
mglearn.discrete_scatter(X_m[:,0],X_m[:,1], assignmeant_m, s=20 ,ax=axes[1])
agg_trm = AgglomerativeClustering(n_clusters=3, linkage='complete')
assignmeant_trm = agg_trm.fit_predict(X_trm)
mglearn.discrete_scatter(X_trm[:,0],X_trm[:,1], assignmeant_trm , s=20 ,ax=axes[2])
agg_r = AgglomerativeClustering(n_clusters=3)
assignmeant_r = agg_r.fit_predict(X_r)
mglearn.discrete_scatter(X_r[:,0],X_r[:,1], assignmeant_r, s=20 ,ax=axes[3])
agg = AgglomerativeClustering(n_clusters=3)
assignmeant = agg.fit_predict(X)
mglearn.discrete_scatter(X[:,0],X[:,1], assignmeant, s=20 ,ax=axes[4])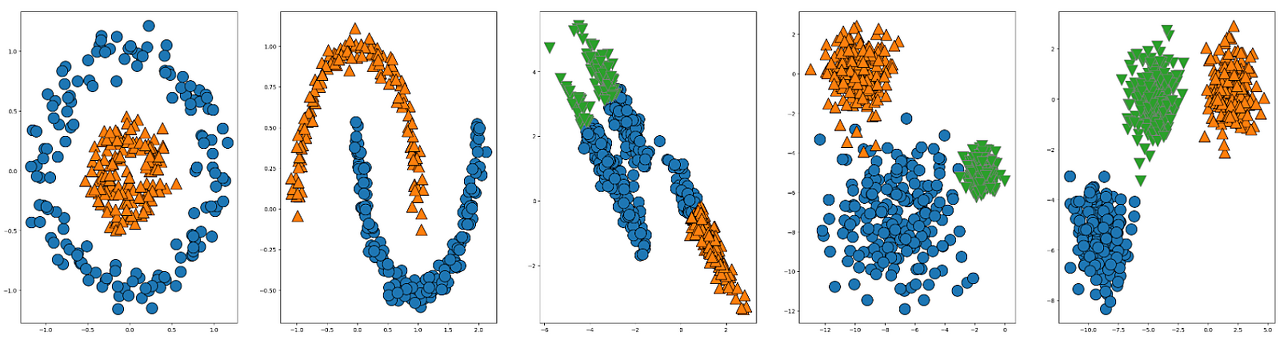
하지만, AgglomerativeClustering는 two_circles 과 two_moons dataset은 군집시킨 것을 확인하실 수 있습니다.
□ AgglomerativeClustering 한계점
하지만, AgglomerativeClustering도 한계점이 있었습니다,,,ㅎㅎ
two_moons dataset을 생성할때에 noise를 0.05에서 0.1로 바꿔 생성하면 군집이 안되고
X_m2,y_m2 = make_moons(n_samples=300, noise=0.1, random_state=0)
# linkage='single'
agg_m2 = AgglomerativeClustering(n_clusters=2, linkage='single')
assignmeant_m2 = agg_m2.fit_predict(X_m2)
mglearn.discrete_scatter(X_m2[:,0],X_m2[:,1], assignmeant_m2)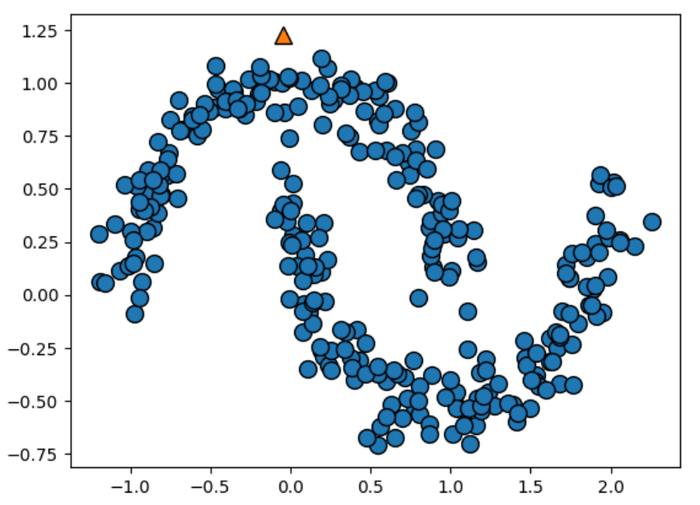
fig, axes = plt.subplots(1,4, figsize=(40,10))
agg = AgglomerativeClustering(n_clusters=3)
assignmeant = agg.fit_predict(X_trm)
mglearn.discrete_scatter(X_trm[:,0],X_trm[:,1], assignmeant, s=20 ,ax=axes[0])
agg1 = AgglomerativeClustering(n_clusters=3, linkage='complete')
assignmeant1 = agg1.fit_predict(X_trm)
mglearn.discrete_scatter(X_trm[:,0],X_trm[:,1], assignmeant1, s=20 ,ax=axes[1])
agg2 = AgglomerativeClustering(n_clusters=3, linkage='average')
assignmeant2 = agg2.fit_predict(X_trm)
mglearn.discrete_scatter(X_trm[:,0],X_trm[:,1], assignmeant2, s=20 ,ax=axes[2])
agg3 = AgglomerativeClustering(n_clusters=3, linkage='single')
assignmeant3 = agg3.fit_predict(X_trm)
mglearn.discrete_scatter(X_trm[:,0],X_trm[:,1], assignmeant3, s=20 ,ax=axes[3])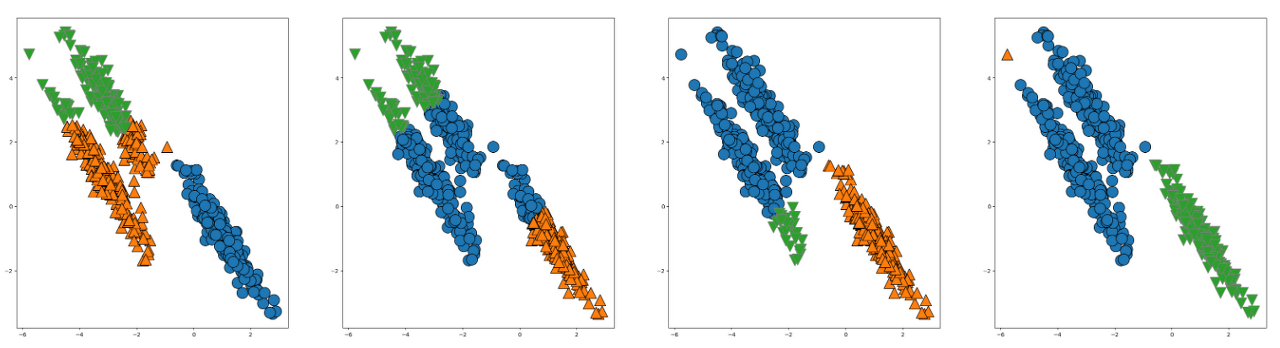
결정적으로, AgglomerativeClustering는 데이터간의 거리를 기반으로 군집시키기때문에 여러분 눈으로는 직관적으로 집단이 보이는 transform 데이터는 군집을 못시키는 모습을 보이네요,, (다른 파라미터값도 바꿔보았지만 군집이 안되네요,,)
이대로 transform 데이터는 군집을 포기해야할까요,,?ㅠㅠ
아니죠! 다음시간에는 보다 더 강력한 군집화 알고리즘 DBSCAN에 대해서 배워보도록 하겠습니다~
이상으로 [Python/ML] Agglomerative Hierarchical Clustering (계층적 군집화)를 마치도록 하겠습니다..
궁금하신 점은 댓글로 질문해주시면 감사하겠습니다~~

참고)
https://scikit-learn.org/stable/modules/generated/sklearn.cluster.AgglomerativeClustering.html?highlight=agglomerative#sklearn.cluster.AgglomerativeClustering
https://process-mining.tistory.com/123
'Data Park > Python' 카테고리의 다른 글
| [Python/ML] SVR (Support Vector Regression) (0) | 2023.02.08 |
|---|---|
| [Python/ML] DBSCAN Clustering (2) | 2023.02.03 |
| [Python/ML] K-MEANS Clustering (0) | 2023.01.27 |
| [Python/ML] K-NN (K-Nearest Neighbors) (0) | 2023.01.10 |
| [Python/ML] SVM (Support Vector Machine) (0) | 2023.01.04 |



