안녕하십니까 데 박 입니다!!
SVM처럼 Decision Tree는 분류와 회귀 작업 그리고 다중출력 작업도 가능한 다재다능한 머신러닝 알고리즘입니다. 또한 작동 방식도 비전공자들이 이해하기 쉽게 학습할 수 있는 간편하고 빠른 알고리즘입니다.
Decision Tree 는 최근에 자주 사용하는 강력한 머신러닝 '앙상블' 알고리즘 중 랜덤포레스트, LightGBM, XGboost의 기본 구성요소이기도 한데요!!
나중에 머신러닝 위주인 실무형 프로젝트를 위해서는 Decision Tree는 "필수"라고 확신합니다!!
□ Decision Tree는 무엇인가
Decision Tree는 분류와 회귀 문제에 널리 사용하는 모델입니다. 기본적으로 결정 트리는 결정에 다다르기 위해 예/아니오 질문을 이어 나가면서 학습합니다.
# 잠깐!!!! mglearn을 install 하셧나요?
!pip install mglearn
# 하셧다면 passs~
import mglearn
mglearn.plots.plot_animal_tree()

이 질문은 스무고개 놀이의 질문과 비슷합니다. 곰, 매, 펭귄, 돌고래라는 네 가지 동물을 구분한다고 생각해봅시다.
우리의 목표는 가능한 한 적은 예/아니오 질문으로 문제를 해결하는 것입니다.
날개가 있는 동물인지를 물어보면 가능성 있는 동물을 둘로 좁힐 수 있습니다.
대답이 “yes”이면 다음엔 독수리와 펭귄을 구분할 수 있는 질문을 해야 합니다. 예를 들면 날 수 있는 동물인지 물어봐야 합니다.
만약 날개가 없다면 가능한 동물은 곰과 돌고래가 될 것입니다.
이제 이 두 동물을 구분하기 위한 질문을 해야 합니다. 예를 들면 지느러미가 있는지를 물어봐야 합니다.
연속된 질문들을 [그림 - 0] 처럼 결정 트리로 나타낼 수 있습니다.
아니,, "이다 or 아니다", "맞다 or 아니다", "있다 or 없다" 로 의사결정을 하는게 참 직관적이고 쉽잖아요? 인정?
오케이 그럼 또!! iris 데이터로 어떻게 작동이 되는지 이해해보도록 하겠습니다!!
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
# 데이터 불러오기
iris = load_iris()
# X, y 할당
X = iris.data
y = iris.target
# 의사결정 나무 모델 생성
tree_clf = DecisionTreeClassifier(max_depth=2, random_state=42)
# 모델 적합
tree_clf.fit(X, y)DecisionTreeClassifier(max_depth=2, random_state=42)또한 트리기반 모델링을 제가 좋아하는 이유는 변수간의 중요도, "Feature Importance"를 출력할 수 있습니다!!
반응변수를 예측하기 위해서 설명변수들이 얼마나 영향을 주는지, 얼마나 중요한지를 시각화할 수도 있습니다!!!!
import seaborn as sns
import numpy as np
%matplotlib inline
# feature importance 추출
print("Feature Importances:\n{0}\n".format(np.round(tree_clf.feature_importances_, 3)))
# feature 별 feature importance 매핑
for name, value in zip(iris.feature_names, tree_clf.feature_importances_):
print('{0}: {1:.3f}'.format(name, value))
# feature importance 시각화
sns.barplot(x=tree_clf.feature_importances_, y=iris.feature_names)
from graphviz import Source
from sklearn.tree import export_graphviz
export_graphviz(
tree_clf,
out_file=os.path.join(IMAGES_PATH, "iris_tree.dot"),
feature_names=iris.feature_names
class_names=iris.target_names,
rounded=True,
filled=True
)
Source.from_file(os.path.join(IMAGES_PATH, "iris_tree.dot"))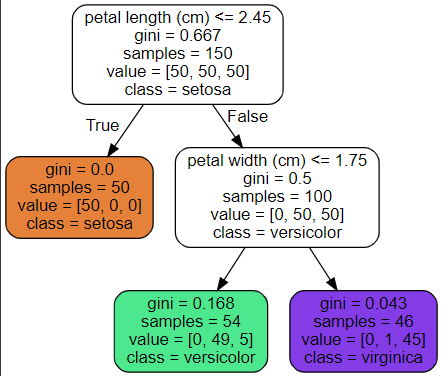
[그림-1]의 트리가 어떻게 예측을 만들어내는지 살펴보겠습니다. 새로 발견한 붓꽃의 품종을 분류하려한다고 가정하겠습니다.
먼저 루트 노드(깊이가 0인 맨 꼭대기의 노드)에서 시작합니다. 이 노드는 곷잎의 길이가 2.45cm보다 짧은지 검사합니다.
만약 그렇다면 루트 노드에서 왼쪽의 자식노드 (깊이1, 왼쪽 노드)로 이동합니다.
이 경우 이 노드가 "리프 노드" (즉, 자식 노드를 가지지 않는 노드)이므로 추가적인 검사를 하지 않습니다.
그냥 노드에 있는 예측 클래스를 보고 결정 트리가 새로 발견한 꽃의 품종을 Iris-Setosa(class=setosa)라고 예측합니다.
또 다른 꽃을 발견했는데 이번에는 꽃입의 길이가 2.45cm보다 깁니다. 이번에는 루트 노드의 오른쪽 자식 노드로 이동해야합니다. 이 노드는 리프 노드가 아니라서 추가로 '꽃잎의 너비가 1.75cm보다 작은지' 검사합니다. 만약 그렇다면 이꽃은 아마도 Iris-Versicolor(깊이 2, 왼쪽)일 것입니다, 그렇지 않다면 Iris-Verginica(깊이 2, 오른쪽)일 것입니다. 아주 간단명료하죠!?
Tip!! 결정트리의 장점은 데이터 전처리가 거의 필요하지 않다는 것입니다.
특성의 표준화 및 정규화를 맞춰주는 원점에 맞추는 작업이 필요하지 않습니다.
(이후에 배울 앙상블 모델도 같은 장점을 갖습니다)
노드의 sample 속성은 얼마나 많은 훈련 샘플이 적용되었는지 헤아린 것입니다.
예를 들어 100개의 훈련 샘플의 꽃잎 길이가 2.45cm보다 길고(깊이 1, 오른쪽), 그중 54개 샘플의 꽃잎 너비가 1.75cm보다 짧습니다(깊이 2, 왼쪽). 노드의 value 속성은 노드에서 각 클래스에 얼마나 많은 훈련 샘플이 있는지 알려줍니다. 맨 오른쪽 아래 노드는 Iris-Setosa가 0개이고 Iris-Versicolor가 1개, Iris-Veiginica가 45개 있습니다.
마지막으로 노드의 gini 속성은 "불순도"를 측정합니다. 한 노드의 모든 샘플이 같은 클래스에 속해 있다면 이 노드를 순수(gini=0)하다고 합니다, 예를 들어 깊이 1의 왼쪽 노드는 Iris-Setosa 훈련 샘플만 가지고 있으므로 순수 노드이고 gini 점수가 0입니다.
from matplotlib.colors import ListedColormap
# X, y 할당
X = iris.data[:, 2:] # 꽃잎 길이와 너비
y = iris.target
# 의사결정 나무 모델 생성
tree_clf = DecisionTreeClassifier(max_depth=2, random_state=42)
# 모델 적합
tree_clf.fit(X, y)
# 결정 경계 plot 함수
def plot_decision_boundary(clf, X, y, axes=[0, 7.5, 0, 3], iris=True, legend=False, plot_training=True):
x1s = np.linspace(axes[0], axes[1], 100)
x2s = np.linspace(axes[2], axes[3], 100)
x1, x2 = np.meshgrid(x1s, x2s)
X_new = np.c_[x1.ravel(), x2.ravel()]
y_pred = clf.predict(X_new).reshape(x1.shape)
custom_cmap = ListedColormap(['#fafab0','#9898ff','#a0faa0'])
plt.contourf(x1, x2, y_pred, cmap=custom_cmap)
if not iris:
custom_cmap2 = ListedColormap(['#7d7d58','#4c4c7f','#507d50'])
plt.contour(x1, x2, y_pred, cmap=custom_cmap2, alpha=0.8)
if plot_training:
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "yo", label="Iris setosa")
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs", label="Iris versicolor")
plt.plot(X[:, 0][y==2], X[:, 1][y==2], "g^", label="Iris virginica")
plt.axis(axes)
if iris:
plt.xlabel("Petal length", fontsize=14)
plt.ylabel("Petal width", fontsize=14)
else:
plt.xlabel(r"$x_1$", fontsize=18)
plt.ylabel(r"$x_2$", fontsize=18, rotation=0)
if legend:
plt.legend(loc="lower right", fontsize=14)
plt.figure(figsize=(8, 4))
plot_decision_boundary(tree_clf, X, y)
plt.plot([2.45, 2.45], [0, 3], "k-", linewidth=2)
plt.plot([2.45, 7.5], [1.75, 1.75], "k--", linewidth=2)
plt.plot([4.95, 4.95], [0, 1.75], "k:", linewidth=2)
plt.plot([4.85, 4.85], [1.75, 3], "k:", linewidth=2)
plt.text(1.40, 1.0, "Depth=0", color='r', fontsize=15)
plt.text(3.2, 1.80, "Depth=1", color='r', fontsize=13)
plt.text(4.05, 0.5, "(Depth=2)", color='r', fontsize=11)
plt.style.use('dark_background')
save_fig("decision_tree_decision_boundaries_plot")
plt.show()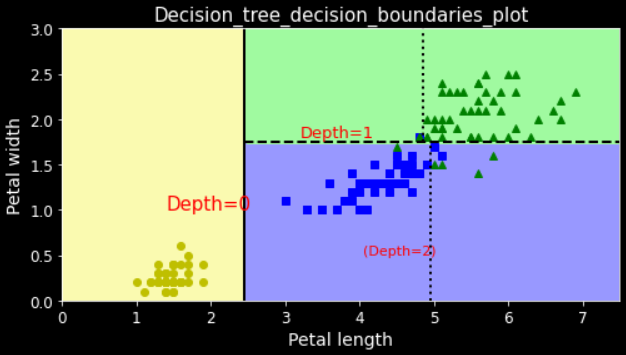
# 클래스 확률 추정
tree_clf.predict_proba([[5, 1.5]])>>> array([[0. , 0.90740741, 0.09259259]])클래스 0일 확률은 0, 클래스 1일 확률은 90.7%, 클래스 2일 확률은 9.2%라고 합니다!!
# 클래스 예측
tree_clf.predict([[5, 1.5]])>>> array([1])클래스 1로 예측되었습니다
□ Decision Tree 파라미터
sklearn.tree.DecisionTreeClassifier
Examples using sklearn.tree.DecisionTreeClassifier: Classifier comparison Classifier comparison Plot the decision surface of decision trees trained on the iris dataset Plot the decision surface of ...
scikit-learn.org
|
Parameter name
|
설명
|
|
min_samples_split
|
- 노드를 분할하기 위한 최소한의 샘플 데이터수 → 과적합을 제어하는데 사용
- Default = 2 → 작게 설정할 수록 분할 노드가 많아져 과적합 가능성 증가
|
|
min_samples_leaf
|
- 리프노드가 되기 위해 필요한 최소한의 샘플 데이터수
- min_samples_split과 함께 과적합 제어 용도
- 불균형 데이터의 경우 특정 클래스의 데이터가 극도로 작을 수 있으므로 작게 설정 필요
|
|
max_features
|
- 최적의 분할을 위해 고려할 최대 feature 개수
- Default = None → 데이터 세트의 모든 피처를 사용
- int형으로 지정 →피처 갯수 / float형으로 지정 →비중
- sqrt 또는 auto : 전체 피처 중 √(피처개수) 만큼 선정
- log : 전체 피처 중 log2(전체 피처 개수) 만큼 선정
|
|
max_depth
|
- 트리의 최대 깊이
- default = None
→ 완벽하게 클래스 값이 결정될 때 까지 분할
또는 데이터 개수가 min_samples_split보다 작아질 때까지 분할
- 깊이가 깊어지면 과적합될 수 있으므로 적절히 제어 필요
|
|
max_leaf_nodes
|
리프노드의 최대 개수
|
□ 규제 parameter
훈련 데이터에 대한 과적합을 피하기 위해 학습할 때 결정 트리의 자유도를 제한 할 필요가 있습니다. 이를 규제(restrictions)라고 합니다. 규제 매개변수는 사용하는 알고리즘에 따라 다르지만, 보통 적어도 결정 트리의 최대 깊이는 제어할 수 있습니다. 사이킷런에서는 max_depth 매개변수로 규제를 조절합니다. (기본값은 제한이 없는 것을 의미하는 None입니다.) max_depth를 줄이면 모델을 규제하게 되고 과대적합의 위험이 감소합니다
DecisionTreeClassifier에는 비슷하게 결정 트리의 형태를 제한 하는 다른 매개변수 (parameter)가 몇개 있습니다. min_samples_split (분할되기 위해 노드가 가져야하는 최소 샘플수),
min_samples_leaf (리프 노드가 가지고 있어야 할 최소 샘플 수),
min_weight_fraction_leaf (min_samples_leaf와 같지만 가중치가 부여된 전체 샘플 수에서의 비율),
max_leaf_nodes (리프 노드의 최대 수),
max_features (각 노드에서 분할에 사용할 특성의 최대 수)가 있습니다.
min_ 으로 시작하는 매개변수를 증가시키거나 max_로 시작하는 매개변수를 감소시키면 모델에 규제가 커집니다.
from sklearn.datasets import make_moons
Xm, ym = make_moons(n_samples=100, noise=0.25, random_state=53)
deep_tree_clf1 = DecisionTreeClassifier(random_state=42)
deep_tree_clf2 = DecisionTreeClassifier(min_samples_leaf=4, random_state=42)
deep_tree_clf1.fit(Xm, ym)
deep_tree_clf2.fit(Xm, ym)
fig, axes = plt.subplots(ncols=2, figsize=(10, 4), sharey=True)
plt.sca(axes[0])
plot_decision_boundary(deep_tree_clf1, Xm, ym, axes=[-1.5, 2.4, -1, 1.5], iris=False)
plt.title("No restrictions", fontsize=16)
plt.sca(axes[1])
plot_decision_boundary(deep_tree_clf2, Xm, ym, axes=[-1.5, 2.4, -1, 1.5], iris=False)
plt.title("min_samples_leaf = {}".format(deep_tree_clf2.min_samples_leaf), fontsize=14)
plt.ylabel("")
save_fig("min_samples_leaf_plot")
plt.show()
[그림 - 3] 아래의 그림은 moons 데이터셋에 훈련시킨 두 개의 결정 트리를 보여줍니다. 왼쪽 결정 트리는 기본 매개변수를 사용하여 훈련시켯고 (즉, 규제가 없음), 오른쪽 결정 트리는 min_samples_leaf=4로 지정하여 훈련시켰습니다. 왼쪽 모델은 확실히 과대적합되었고 오른쪽 모델은 일반화 성능이 더 좋을 것 같아 보입니다.
□ Decision Tree의 단점
아마 결정 트리가 장점이 많다는 것을 알게 되었을 것입니다. 결정트리는 이해하고 해석하기 쉬우며, 사용하기 편하고 여러 용도로 사용할 수 있습니다.
하지만 몇가지 단점이 있습니다. 규제 파라미터를 설정하지않으면 과적합될 위험이 크고, 결정 트리는 계단 모양의 결정 경계를 만듭니다.
np.random.seed(6)
Xs = np.random.rand(100, 2) - 0.5
ys = (Xs[:, 0] > 0).astype(np.float32) * 2
angle = np.pi / 4
rotation_matrix = np.array([[np.cos(angle), -np.sin(angle)], [np.sin(angle), np.cos(angle)]])
Xsr = Xs.dot(rotation_matrix)
tree_clf_s = DecisionTreeClassifier(random_state=42)
tree_clf_s.fit(Xs, ys)
tree_clf_sr = DecisionTreeClassifier(random_state=42)
tree_clf_sr.fit(Xsr, ys)
fig, axes = plt.subplots(ncols=2, figsize=(10, 4), sharey=True)
plt.sca(axes[0])
plot_decision_boundary(tree_clf_s, Xs, ys, axes=[-0.7, 0.7, -0.7, 0.7], iris=False)
plt.sca(axes[1])
plt.title("")
plot_decision_boundary(tree_clf_sr, Xsr, ys, axes=[-0.7, 0.7, -0.7, 0.7], iris=False)
plt.ylabel("")
plt.show()
그래서 훈련 세트의 회전에 민감합니다. [그림 - 4]은 간단한 선형으로 구분될 수 있는 데이터셋을 예로 보여줍니다. 왼쪽의 결정 트리는 쉽게 데이터셋을 분류하지만, 데이터셋을 45도 회전한 오른쪽의 결정 트리는 불필요하게 구불구불해졌습니다.
두 결정 트리 모두 훈련 세트를 완벽하게 학습하지만 오른쪽 모델을 잘 일발화될 것 같지 않습니다.
이런 문제를 해결하는 한가지 방법은 훈련 데이터를 더 좋은 방향으로 회전시키는 PCA 기법을 사용하는 것입니다.
다음 장에서 보게 될 랜덤 포레스트는 많은 트리에서 만든 예측을 평균으로 이런 불안정성으로 극복할 수 있습니다!
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifier
from sklearn.metrics import accuracy_score
tree_clf = DecisionTreeClassifier(random_state=42)
tree_clf.fit(X_train, y_train)
y_pred_tree = tree_clf.predict(X_test)
print(accuracy_score(y_test, y_pred_tree))
bag_clf = BaggingClassifier(
DecisionTreeClassifier(), n_estimators=500,
max_samples=100, bootstrap=True, random_state=42)
bag_clf.fit(X_train, y_train)
y_pred = bag_clf.predict(X_test)
print(accuracy_score(y_test, y_pred))>>> 배깅 accuracy : 0.904
>>> 의사결정나무 accuracy : 0.856결정경계는 배깅을 사용한 의사결정 나무가 더 일반적으로 나옵니다!!
from matplotlib.colors import ListedColormap
plt.style.use('dark_background')
def plot_decision_boundary(clf, X, y, axes=[-1.5, 2.45, -1, 1.5], alpha=0.5, contour=True):
x1s = np.linspace(axes[0], axes[1], 100)
x2s = np.linspace(axes[2], axes[3], 100)
x1, x2 = np.meshgrid(x1s, x2s)
X_new = np.c_[x1.ravel(), x2.ravel()]
y_pred = clf.predict(X_new).reshape(x1.shape)
custom_cmap = ListedColormap(['#FFD8D8','#9898ff','#B2EBF4'])
plt.contourf(x1, x2, y_pred, #alpha=0.3,
cmap=custom_cmap)
if contour:
custom_cmap2 = ListedColormap(['#7d7d58','#4c4c7f','#507d50'])
plt.contour(x1, x2, y_pred, #alpha=0.8,
cmap=custom_cmap2)
plt.plot(X[:, 0][y==0], X[:, 1][y==0], "ro", alpha=alpha)
plt.plot(X[:, 0][y==1], X[:, 1][y==1], "bs", alpha=alpha)
plt.axis(axes)
plt.xlabel(r"$x_1$", fontsize=18)
plt.ylabel(r"$x_2$", fontsize=18, rotation=0)
fig, axes = plt.subplots(ncols=2, figsize=(12,6), sharey=True)
plt.sca(axes[0])
plot_decision_boundary(tree_clf, X, y)
plt.title("Decision Tree", fontsize=18)
plt.sca(axes[1])
plot_decision_boundary(bag_clf, X, y)
plt.title("Decision Trees with Bagging", fontsize=18)
plt.ylabel("")
plt.show()
이상으로 [Python/ML_Classification] Decision Tree 를 마치도록 하겠습니다..
궁금하신 부분이나 질문은 댓글로 남겨주시면 되겠고, 오늘도 긴 글 읽어주셔서 대단히 감사드립니다!
'Data Park > Python' 카테고리의 다른 글
| [Python/ML] K-MEANS Clustering (0) | 2023.01.27 |
|---|---|
| [Python/ML] K-NN (K-Nearest Neighbors) (0) | 2023.01.10 |
| [Python/ML] SVM (Support Vector Machine) (0) | 2023.01.04 |
| [Python/ML] Ada Boosting, Gradient Boosting (0) | 2022.12.11 |
| [Python/ML] Random Forest (랜덤 포레스트) (1) | 2022.12.10 |



